Hello आज हम इस पोस्ट में जानेंगे वर्गमूल क्या है वर्गमूल निकालने का सूत्र एवं वर्गमूल कैसे निकाले (vargmul kaise nikale) और वर्गमूल ज्ञात करने की विधियां की पूरी जानकारी।
अक्सर गणित विषय से सम्बंधित प्रश्न को हल करने के लिए वर्गमूल (Square root) की आवश्यकता पड़ती है, ऐसे में वर्गमूल का ज्ञान सही से न होने के कारण या वर्ग निकालने की विधि ज्ञात न होने के कारण बहुत से छात्र/छात्राएं वर्गमूल से जुड़े बहुत से सरल सवालों को खाली छोड़ आते है।
इस लिए निचे हम आपको 1 से 100 तक वर्गमूल लिस्ट – square 1 to 100 लेकर आए है जिन्हें आप आसानी से याद कर सकते है। जिसका उपयोग आप वर्गमूल से सम्बंधित सवाल बनाते समय कर पाएंगे।
उससे पहले चलिए जानते है की वर्गमूल क्या है? उसकी पूरी जानकारी विस्तार में चलिए जानते है।
वर्गमूल क्या है?
ऐसी संख्या जिसको परस्पर दो बार गुणा करने पर जो संख्या निकलती है वह वर्गमूल कहलाती है, इसे √ के चिन्ह से भी दिखाया जाता है।
जैसे:
25 का वर्गमूल = √25 = 5
144 का वर्गमूल = √144 = 12
625 का वर्गमूल = √625 = 25
Vargmul kaise nikale | वर्गमूल कैसे निकाले ?
वर्गमूल निकालने का सबसे आसान तरीका है की आपको जिस भी संख्या का वर्ग निकालना है उसको दो बार गुणा कर देना है, जिसके बाद आपको पूर्ण वर्गमूल निकल आएगा
| 1×1 = 1 | 10×10 = 100 |
| 2×2 = 4 | 20×20 = 400 |
| 3×3 = 9 | 30×30 = 900 |
| 4×4 = 16 | 40×40 = 1600 |
| 5×5 = 25 | 50×50 = 2500 |
| 6×6 = 36 | 60×60 = 3600 |
| 7×7 = 49 | 70×70 = 4900 |
| 8×8 = 64 | 80×80 = 6400 |
| 9×9 = 81 | 90×90 = 8100 |
वर्गमूल ज्ञात करने की विधियां
सामान्यतः किसी भी संख्या का वर्ग या वर्गमूल आप निम्न दो विधियों से निकाल सकते है। हालाँकि निचे हमने vargmul question भी बताए है जिसकी मदद से आप वर्गमूल निकालना सीख पाएंगे.
- गुणनखंड विधि द्वारा
- भागफल विधि द्वारा
1. गुणनखंड विधि द्वारा:
इस विधि में किसी संख्या को छोटे – छोटे गुणनखंड में विभाजित करके प्रत्येक संख्या का जोड़ा बनाते है, और सभी जोड़ो में से एक संख्या लेकर उसे गुणा करने पर प्राप्त संख्या वर्गमूल कहलाती है।
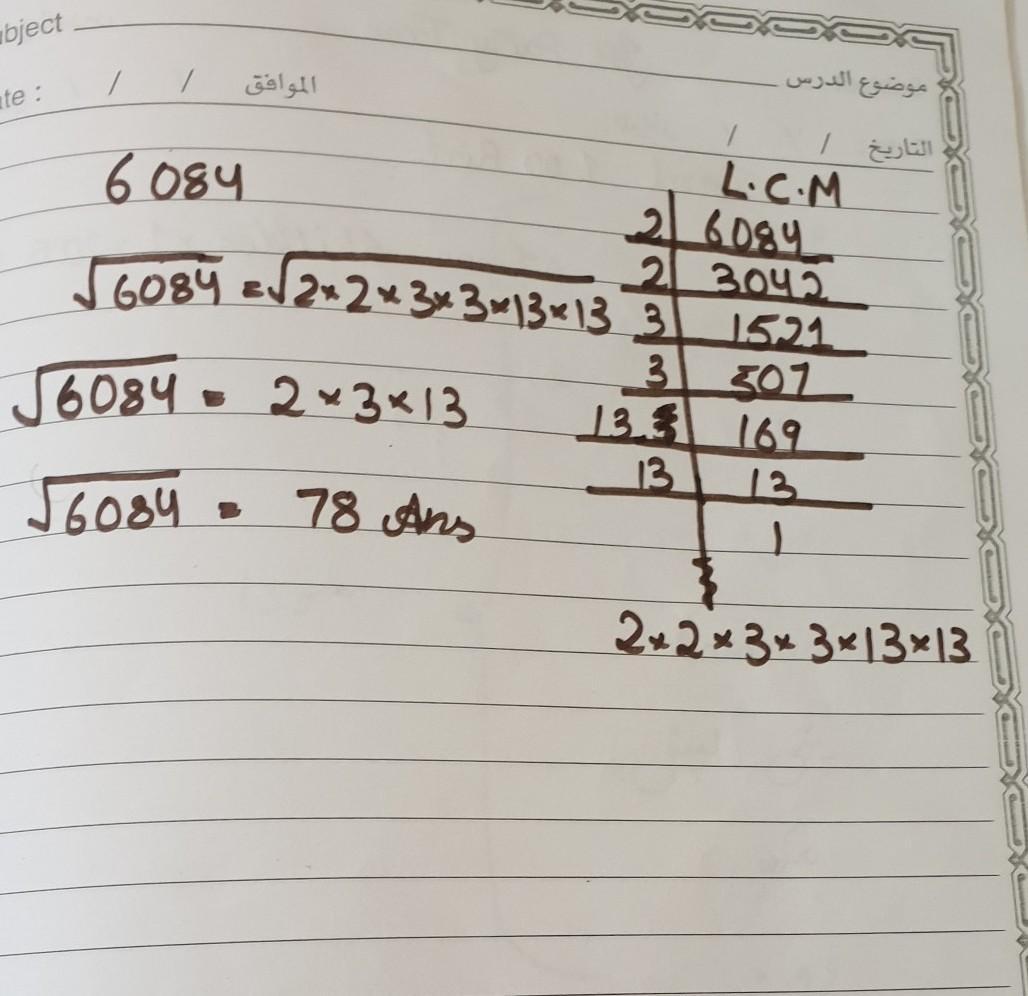
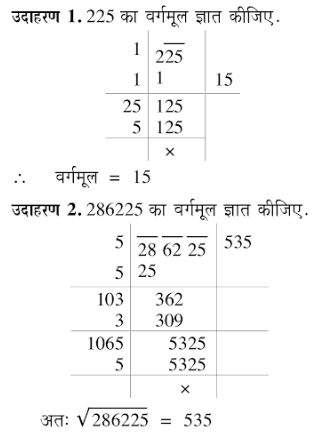
2. भागफल विधि द्वारा:
भाग विधि से वर्गमूल निकालने के लिए आप निचे बताये हुए Question की मदद से भागफल विधि से वर्गमूल ज्ञात कर सकते है।
इसके अलावा यदि ऊपर के दो विधि को नहीं अपनाना चाहते है तो आप निचे दिए 1 से 100 तक के वर्गमूल को याद कर सकते है।
- ब्याज कैसे निकाले? ब्याज निकालने का फार्मूला
- आयत का क्षेत्रफल और परिमाप कैसे निकाले?
- भारत देश के राज्य और उनकी राजधानी के नाम जानियें ।
1 से 100 तक के वर्गमूल – Square root 1 to 100
- 1² – 1
- 2² – 4
- 3² – 9
- 4² – 16
- 5² – 25
- 6² – 36
- 7² – 49
- 8² – 64
- 9² – 81
- 10² – 100
- 11² – 121
- 12² – 144
- 13² – 169
- 14² – 196
- 15² – 225
- 16² – 256
- 17² – 289
- 18² – 324
- 19² – 361
- 20² – 400
- 21² – 441
- 22² – 484
- 23² – 529
- 24² – 576
- 25² – 625
- 26² – 676
- 27² – 729
- 28² – 784
- 29² – 841
- 30² – 900
- 31² – 961
- 32² – 1024
- 33² – 1089
- 34² – 1156
- 35² – 1225
- 36² – 1296
- 37² – 1369
- 38² – 1444
- 39² – 1521
- 40² – 1600
- 41² – 1681
- 42² – 1764
- 43² – 1849
- 44² – 1936
- 45² – 2025
- 46² – 2116
- 47²- 2209
- 48² – 2304
- 49² – 2401
- 50² – 2500
- 51² – 2601
- 52² – 2704
- 53² – 2809
- 54² – 2916
- 55² – 3025
- 56² – 3136
- 57² – 3249
- 58² – 3364
- 59² – 3481
- 60² – 3600
- 61² – 3,721
- 62² – 3,844
- 63² – 3,969
- 64² – 4,096
- 65² – 4,225
- 66² – 4,356
- 67² – 4,489
- 68² – 4,624
- 69² – 4,761
- 70² – 4,900
- 71² – 5,041
- 72² – 5,184
- 73² – 5,329
- 74² – 5,476
- 75² – 5,625
- 76² – 5,776
- 77² – 5,929
- 78² – 6,084
- 79² – 6,241
- 80² – 6,400
- 81² – 6,561
- 82² – 6,724
- 83² – 6,889
- 84² – 7,056
- 85² – 7,225
- 86² – 7,396
- 87² – 7,569
- 88² – 7,744
- 89² – 7,921
- 90² – 8,100
- 91²- 8,281
- 92² – 8,464
- 93² – 8,649
- 94² – 8,836
- 95² – 9,025
- 96² – 9,216
- 97² – 9,409
- 98² – 9,604
- 99² – 9,801
- 100² – 10,000
Conclusion
मुझे उम्मीद है की आपको इस आर्टिकल की मदद से वर्गमूल कैसे कहते है, वर्गमूल कैसे निकाले, वर्गमूल निकालने की विधियां और 1 से 100 तक के वर्गमूल जानने व सिखने को मिल चूका होगा।
यदि आपको यह आर्टिकल vargmul kaise nikale अच्छी लगी हो तो इसे अपने दोस्तों के साथ जरुर शेयर करें।
साथ ही हमसे सोशल मीडिया पर जुड़ने के लिए फेसबुक और ट्विटर पर फॉलो जरुर करें, और हमारे YouTube Channel को भी सब्सक्राइब जरुर कर लें।
इसे जरुर पढ़ें:
- Table 2 to 20 | Multiplication Table Chart PDF Download
- Most Important Full Form list
- Computer क्या है, यह कितने प्रकार के होते है?
- Aadhar Card कैसे निकाले?
- Net Banking Kaise Kare